Design of gapped k-mer seeds

Investigators: Kamalika Ray & Sven Rahmann
Funding: internal

We develop methods for optimizing gapped k-mer seeds with regard to beneficial properties, such as tolerance towards mismatches in a sequenced read.

Gapped k-mers

Given a sequence s, a gapped k-mer is a subsequence of s of length k, whose characters have been selected according to a given pattern (mask) of length w that consists of k significant and (w-k) insignificant positions (gaps).

An example is ##_#__#___##___#__#_## with k=10 and w=22, where # denotes a significant position.

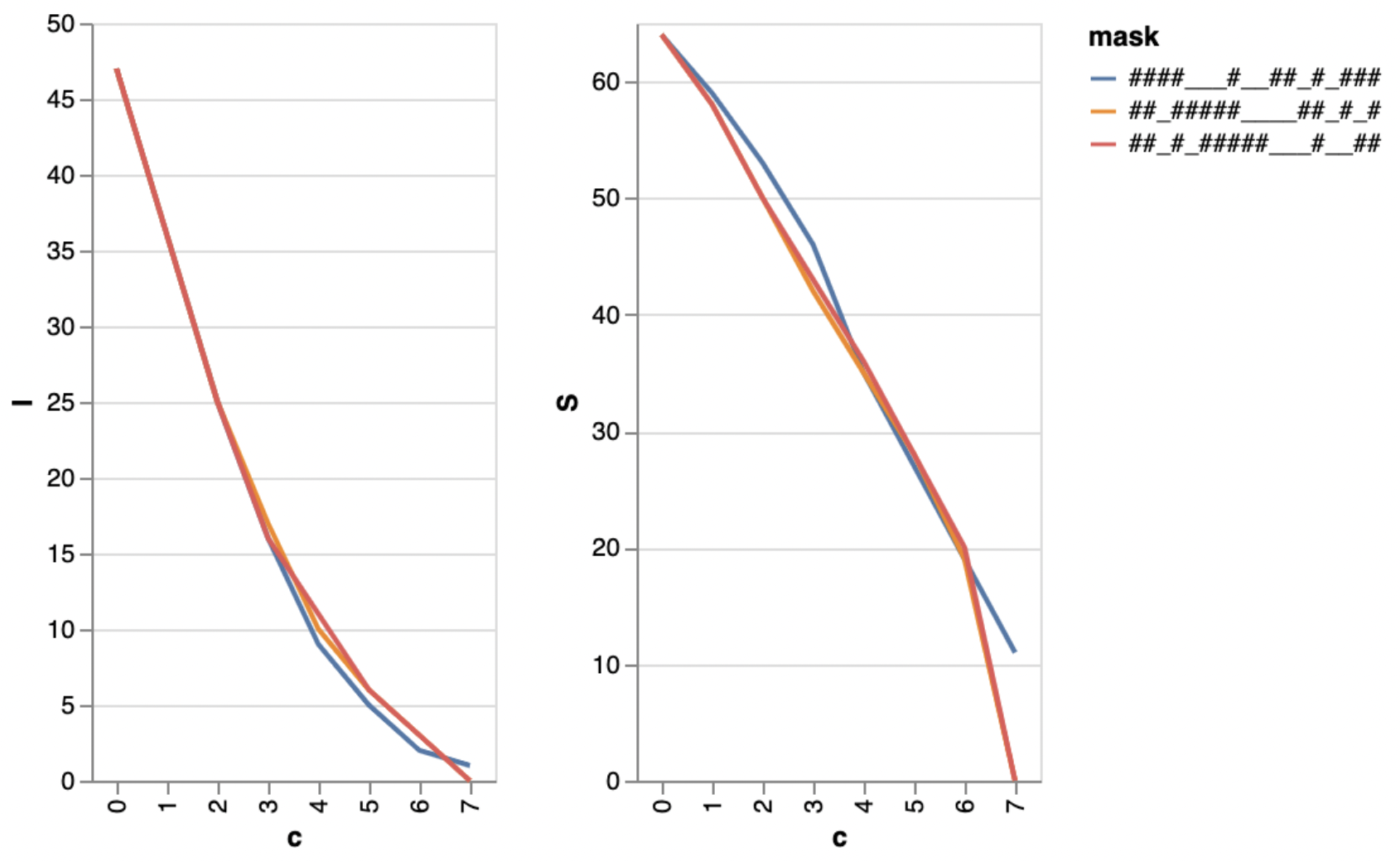
The design problem

Given a sequenced DNA read of length n and a total of c substitutions that can be placed arbitrarily (in particular, adversarily) in the read, how many of the gapped k-meres are changed by the c substitutions in the worst case? In other words, for a given mask like the example above, find the worst-case placement of substitutions to change as many of the gapped k-mers as possible.

Among all masks of the same shape (w,k), find the best mask that leaves as many k-mers unchanged (in the worst case) as possible. A related, question is, among all masks, maximize the reads’s worst-case coverage by gapped k-mers.

Both questions can be answered with the help of integer linear programming and by analyzing the structure of the solutions.

Applications

We can replace standard k-mers used in many alignment-free methods by optimal gapped k-mers and guarantee better sensitivity/selectivity properties.

Publications

(in preparation)