Mathematics of diversity

Investigators: Sven Rahmann
Funding: internal
Software: dupre

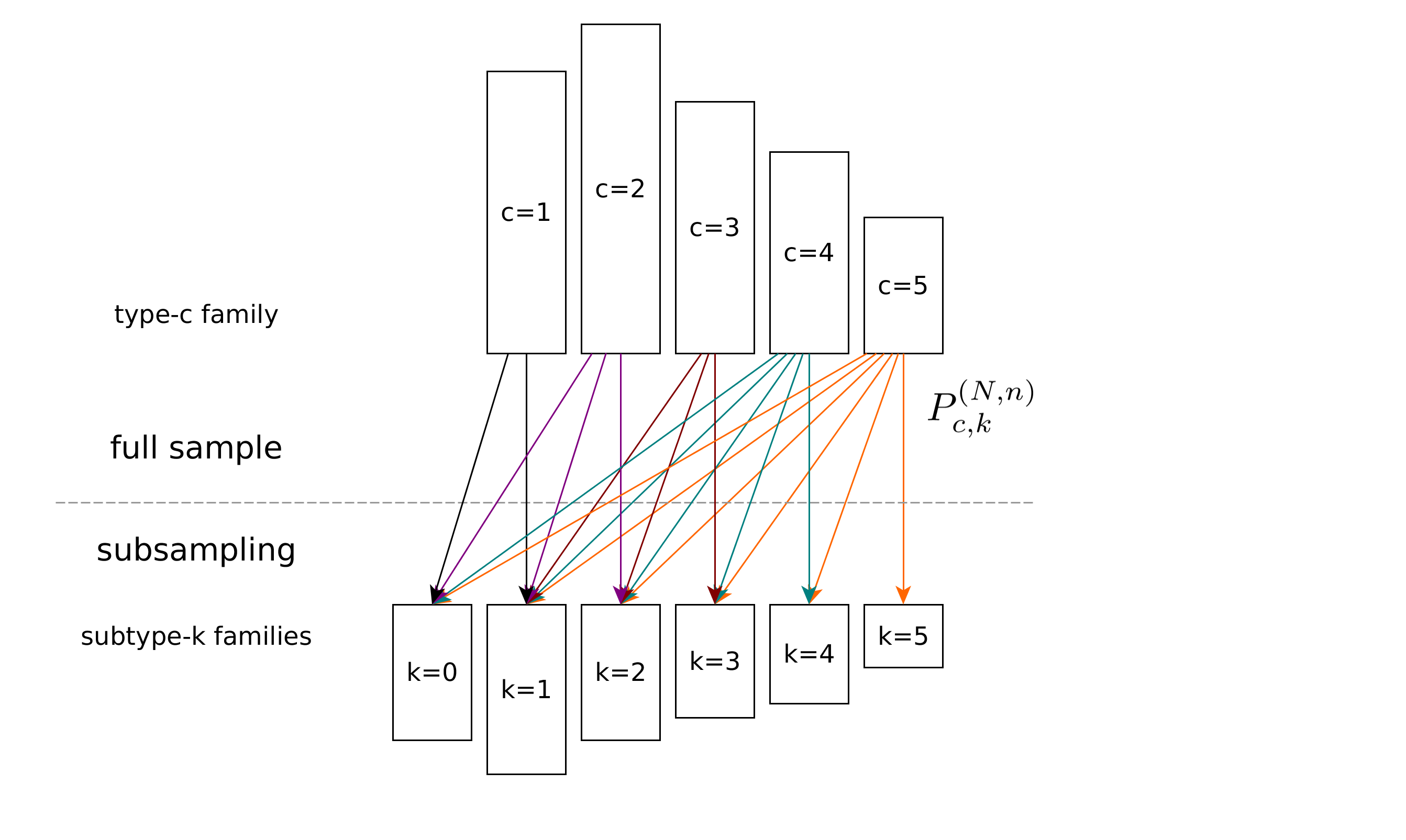
In this project, we investigate the diversity of large populations when only a small subsample can be observed.

A special case is the duplicate rate of a sequencing library: In high-throughput sequencing (HTS) projects, the sequenced fragments’ duplicate rate is a key quality metric. A high duplicate rate may arise from a low amount of input DNA and many PCR cycles. Many methods for downstream analyses require that duplicates be removed. If the duplicate rate is high, most of the sequencing effort and money spent would have been in vain. Therefore, it is of considerable interest to estimate the duplicate rate after sequencing only a small subsample at low depth (multiplexed with other libraries) for quality control before running the full experiment. The problem is equal to the library complexity problem, which has numerous use cases, e.g. the prediction of species in an ecosystem or the estimation of different cells in tissues by taking subsamples.

We developed an elementary mathematical framework and an efficient computational approach based on quadratic and linear optimization to estimate the complexity and duplication rate from a small subsample. Our method is based on up-sampling the occupancy distribution of the reads’ copy numbers. Compared to an existing approach, we use an explicit and easily explained mathematical model that accurately inverts the subsampling process.